# 二进制
生活中,我们习惯使用的有十进制,另外还有八进制、十二进制、十六进制、六十进制等等,而计算机使用的是二进制。
二进制(binary)在数学和数字电路中是指以 2 为基数的记数系统。在这一系统中,通常使用两个不同的符号 0(代表零)和 1(代表一)来表示。
由于二进制中只有两个数字 0 和 1,所以很容易用电子元件的两种状态来表示(如电平的高或低,晶体管的导通或截止),所以二进制具有硬件上容易实现、运算规则简单、便于机器执行等优点。
但是,二进制也存在着位数长、书写和阅读都不方便且容易出错等缺点。有时八进制和十六进制能方便地与二进制实现转换,所以常用八进制十六进制进行输入或输出。
# 进位计数制
诸如二进制之类的进制,它们到底是依据什么来进行定义的呢?
我们经常需要用数目来表示的一个量的多少,而一个量用数目表示出来的多少,实际上就是这个量的数值。
用一组固定的符号和统一的规则来表示数值的方法,称为数制,也称为“计数制”。若按进位的方法进行计数,则称为进位计数制。
任何一个数制都包含两个基本要素(基数和位权),而每一种进位计数制包含一组数码符号和三个基本因素:
- 数码:一组用来表示某种数制的符号(二进制:0、1,十进制:0、1、2、3、4、5、6、7、8、9)。
- 基数:某数制可以使用的数码个数(二进制:2,十进制:10)。
- 数位:数码在一个数中所处的位置(如十进制的 123 中的 1 的数位为 2)。
- 位权:权是基数的幂,表示数码在不同位置上的数值(如十进制的 123 中 1 的位权是 100,2 的位权是 10)。
进位计数制采用位权表示法:在一个数字当中, 每个数位上的数码所代表的数值的大小,等于在这个数位上的数码乘上对应的位权。
所以说,位权和基数则是进位计数制中的两个要素。
同时,进位计数制还具有逢 N 进一的基本特点(N 是指进位计数制表示一位数所需要的符号数目)。
# 进制转换
所谓进制转换,就是将一种进制的数字转换为另一种进制的数字。数字的表示形式虽然改变了,但是数字的值并没有变。
R 进制转为十进制的:按“权”展开,然后各项相加:
$a_mr^m + a_{m-1}r^{m-1} + ... + a_1r^1 + a_0r^0 + ... + a_{n-1}*r^{-n+1} + a_{n}*r^{-n}$
例如:
$(1111.11)_2=1x2^3 + 1x2^2 + 1x2^1 + 1x2^0 = 15.75$
反过来,十进制转换成 R 进制:对整数部分进行除 R 取余数,直至商为零,余数倒序排序;对小数部分进行乘 R 取整,然后将结果从上到下排列;最后通过小数点组合得到的两部分。
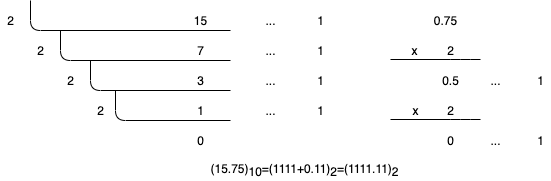
对于其它进制之间的转换则可以先转换成十进制,然后再转换成需要的进制。
# 有符号数的表示
各种字母、数字符号的组合、语音、图形、图像等在在计算机系统中都称为数据,它们都可以被简单的分为数值数据和非数值数据。
数值数据是指通常所说的数或数据,它有正负和大小之分,也有整数和小数之分。
由于在计算机中不能存储负号,所以对于有符号数的正负需要通过 0 或者 1 来进行表示。一般指定最左边的一位为 0 来代表正数,为 1 来代表负数。
若一个数用 8 为二进制来表示,正 6 和-6 分别表示为 00000110 和 10000110。
这种用 0 和 1 表示数的符号的数为机器数(原码),但实际上计算机中并不是用这种方法存储有符号数的。为什么呢?
因为机器数在进行运算时,若将符号位和数值位同时参与运算,则会得出错误的结果。比如一个正数加上一个绝对值更小的负数,得到的结果却是负数。
# 反码和补码
为了解决有符号数的运算问题,计算机中引入了反码和补码的概念,将加减法运算统一转换为补码的加减运算。
整数的原码表示是整数的符号位用 0 表示正,1 表示负,其数值部分是该数的绝对值的二进制表示。
反码是求补码的中间过度,它表示是对该数的原码除了符号位外各位取反。在原码和反码中 0 有两种表示方式,即 00000000 和 10000000。
负数的补码则是在其反码的基础上末位加 1,而正数的原码、反码和补码形式完全相同。
在补码表示中,0 有唯一的表示形式。因此,可以用多出来的编码 10000000 来扩展补码的表示范围为 -128。最高位 1 可看作是符号位负数,又可表示为数值。
现在在加减运算中,减去一个数实际上就等于加上这个数的补码。
# 定点数与浮点数
数值数据中除了整数外还包含小数,对于带有小数点的数字在计算机中可以有两种方法表示:定点数和浮点数。
定点数是指规定小数点固定在某一位置上,包括有定点整数(纯整数,小数点位固定在最后一位之后)和定点小数(纯小数,小数点固定在最高位之后)。
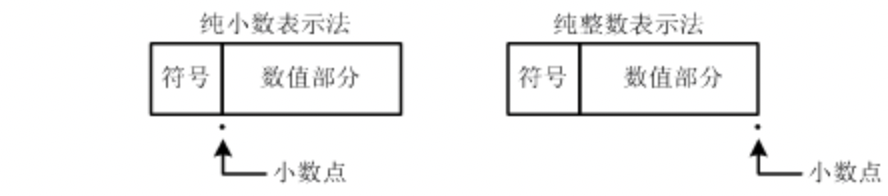
比如 8 位字长的纯小数,第一位为符号位,小数点在第一位后面,后七位为具体数值,如: -0.1001 原码表示为 1.1001,反码为 1.0110,补码为 1.0111。
浮点数则是指一个数的小数点的位置不是固定的,可以进行浮动。
在计算机中,浮点数用以近似表示任意某个实数,并采用以 2 为底的科学记数法进行存储:
$N=数符尾数2^{阶码}$
其中,数符为 0 表示正,为 1 表示负,尾数(对应的位数决定了数的精度)和阶码(对应的位数决定了数的范围)都用二进制数进行表示。
# 单精度与双精度
在 IEEE-754 标准出现之前,业界并没有一个统一的浮点数标准,相反,很多计算机制造商都在设计自己的浮点数规则以及运算细节。
为了便于软件的移植,浮点数的表示格式应该有一个统一的标准。1985 年,IEEE(Institute of Electrical and Electronics Engineers,美国电气和电子工程师协会)提出了 IEEE-754 标准,并以此作为浮点数表示格式的统一标准。
IEEE 标准从逻辑上采用一个三元组 {S, E, M} 来表示一个数 N,它规定基数为 2,符号位 S 用 0 和 1 分别表示正和负,尾数 M 用原码表示,阶码 E 用移码表示。
根据浮点数的规格化方法,尾数域的最高有效位总是 1,由此,该标准约定这一位不予存储,而是认为隐藏在小数点的左边,因此,尾数域所表示的值是 1.M(实际存储的是 M),这样可使尾数的表示范围比实际存储多一位。
同时,为了表示指数的正负,阶码 E 通常采用移码方式来表示,将数据的指数加上一个固定的偏移量($2^{e-1}-1$,其中的 e 为存储指数的比特的长度)后作为该数的阶码,这样做既可避免出现正负指数,又可保持数据的原有大小顺序,便于进行比较操作。
目前,IEEE 754 规定了四种表示浮点数值的方式,我们常见的两种方式是单精确度以及双精确度:
| 方式 | 数符(s) | 阶码(E) | 尾数(M) | 总位数 |
|---|---|---|---|---|
| 单精度 | 1 位 | 8 位 | 23 位 | 32 位 |
| 双精度 | 1 位 | 11 位 | 52 位 | 64 位 |
# 字符编码
除了数值数据外,计算机中还存储着字符、语音、图形、图像等资源。在计算机中,所有的数据在存储和运算时都要使用二进制数表示。
以英文字母为例,在计算机中存储时也要使用二进制数来表示,而具体用哪些二进制数字表示哪个符号,当然每个人都可以约定自己的一套(这就叫编码)。
和浮点数的规则一样,如果要想互相通信而不造成混乱,那么大家就必须使用相同的编码规则,于是美国有关的标准化组织就出台了 ASCII 编码。
标准 ASCII 码也叫基础 ASCII 码,使用 7 位二进制数(剩下的 1 位二进制为 0)来表示所有的大写和小写字母,数字 0 到 9、标点符号,以及在美式英语中使用的特殊控制字符。
为了能在计算机中使用汉字,1980 年,我国颁布了汉字编码的国家标准:GB2312-80《信息交换用汉字编码字符集》基本集,规定了在不同的汉字系统中进行汉字交换时使用的编码,简称国标码。
在国标码中对 6763 个常用汉字规定了二进制编码,每个汉字使用 2 个字节,以 16 进制进行表示。
当系统中同时存在 ASCII 码和汉字国标码时,将会产生二义性。因此引入了汉字机内码(又称“汉字 ASCII 码”,简称“内码”,指计算机内部存储,处理加工和传输汉字时所用的由 0 和 1 符号组成的代码)来保证中西文的兼容。
随着计算机技术的发展,社会应用已较为普及,6763 个汉字已经无法满足社会信息化的要求。为了兼容 GB2312,同时解决信息系统用字不足的问题,在 1995 年发布了 GBK《汉字内码扩展规范》。
GBK 总计 23940 个码位,共收入 21886 个汉字和图形符号,采用了单双字节变长编码(英文使用单字节编码,完全兼容 ASCII 字符编码,中文部分采用双字节编码)。
继 GBK 之后,我国后续又推出了 GB18030 编码方案,此方案包含多种我国少数民族文字(如藏、蒙古、傣、彝、朝鲜、维吾尔文等)的超大型中文编码字符集强制性标准,其中收入汉字 70000 有余。
# UTF-8
如果各个国家都发布一套属于自己的编码标准,那么互相之间谁也无法明白。为了统一所有文字的编码,Unicode 应运而生。
Unicode 从 0 开始,为每个符号指定一个编号,这叫做"码点"(code point)。由于只规定了每个字符的码点,到底用什么样的字节序表示这个码点,就涉及到编码方法。
最直观的编码方法是,每个码点使用四个字节表示,字节内容一一对应码点。这种编码方法就叫做 UTF-32。
虽然 UTF-32 的转换规则简单直观,查找效率高,但空间浪费严重。比如同样内容的英语文本,它会比 ASCII 编码大四倍,所以我们见得更多的是 UTF-8 编码。
UTF-8 是一种变长的编码方法,字符长度从 1 个字节到 4 个字节不等。越是常用的字符,字节越短,最前面的 128 个字符,只使用 1 个字节表示,与 ASCII 码完全相同。
存在与 UTF-32 与 UTF-8 之间的是 UTF-16 编码,它规定基本平面的字符占用 2 个字节,辅助平面的字符占用 4 个字节。
由于在在 JavaScript 语言出现的时候还没有 UTF-16 编码,因此采用了 UCS-2 编码(使用 2 个字节表示当时已有码点的字符)。
从 ES6 开始,JavaScript 大幅增强了 Unicode 支持,基本上解决了识别 4 字节码点的问题。
# 多媒体信息编码
多媒体信息是指以文字、声音、图形、图像为载体的信息。计算机除了能够处理、存储数值和文字,还能处理大量多媒体信息。这些多媒体信息虽然形式不同,但进入到计算机中都要转化为二进制形式表示。
多媒体处理技术的实质就是将自然形式存在的图像、声音和视频等媒体数字化,然后利用计算机技术对这些数字进行处理,并以一种友好的方式提供给用户使用。
# 图形图像
| 名称 | 概念 | 存储方式 | 特点 |
|---|---|---|---|
| 图形 | 通过绘图软件绘制的图,以矢量图形文件形式存储 | 矢量图形存储的是一组描述各个图元的大小、位置、形状、颜色等属性的指令集合 | 占用空间小,对图放大、缩小、移动、旋转不失真 不必进行数字化处理,以位图形式存储 |
| 图像 | 由扫描仪、数码相机、数码摄像机等输入设备捕捉的真实场景画面产生的映像,以位图形式存储 | 位图存储的是构成图像每个像素的亮度、颜色,位图的大小与分辨率大小和色彩种类有关 | 位图经过放大、缩小会出现失真,不清晰,占用的存储空间比矢量图大 经过采样、量化处理 |
常见的图形图像文件格式:
| 扩展名 | 特点 |
|---|---|
| BMP | 位图格式文件,图形与图像通用,不压缩,占用磁盘空间大,适合单机使用 |
| GIF | 压缩比高,磁盘空间占用小,适合网上传输交换,不能存储超过 256 色图像,可以包含动画的图片文件 |
| TIF | 支持压缩与非压缩,适合不同平台之间图像交换 |
| JPEG,JPG | 压缩比高,占用磁盘空间小,适合大量图像处理,网络传输 |
| WMF | Windows 剪贴板及印刷出版领域使用,属于矢量图形 |
| PNG | 流式图像文件,压缩比高,无损压缩,适合网上传输,支持 Alpha 通道图像制作,不支持动画功能 |
# 声音
声音是一种采用模拟的连续波形表示,称为声波。
波形的最高点(最低点)到基线点的距离称为振幅,表示声音的大小(音量)。振幅越大,声音就越响,反之声音就越轻。
频率的高低表示声音音调的高低(我们平时称之为高音、低音),两波峰之间的距离越近,声音越尖锐(平时称之为高音),反之声音越低沉(平时称之为低音)。
要讲模拟信号转换为数字信号也要经过采样和量化。记录每秒钟存储声音数据量的公式:
$每秒数据量(字节) = 采样频率(Hz) x 采样精度(bit) / 8 * 声道数$
常见的声音文件格式:
| 扩展名 | 特点 |
|---|---|
| WAV | 记录真实声音,对存储空间需求太大,不便于交流和传播,是 Windows 系统使用的标准数字音频波形文件 |
| MIDI | 比波形文件小,节省空间,但缺乏重现真实自然声音的能力,常用来存放背景音乐 |
| WMA | 与 MP3 格式类似的一种新的音频格式,压缩比和音频方面都超过 MP3,适合网络实时低速率传输 |
| MP3、MP4 | 数字音频编码和有损压缩格式,压缩比高,基本不失真 |
# 视频
视频信号数字化的原理和音频信息数字化相似,以一定的频率对单帧视频信号进行采样、量化等,实现模数转换、彩色空间变换和编码压缩等。
常用的视频文件和流媒体文件格式:
| 扩展名 | 特点 |
|---|---|
| AVI | 采用有损压缩、压缩比高,解决了音频与视频信息的同步问题,已成为 Windows 视频文件的标准,用于保存电影、电视信息 |
| MPG | 按照 MPEG 标准压缩的全视频文件 |
| WMV | 独立于编码方式的标准,可以直接在网上实时观看视频,属于网络流媒体,播放器是 Media Player |
| rm | 压缩比高,文件小、适合网络传输,属于流媒体文件格式,文件的播放器是 RealPlayer |
| ASF | 可以直接在网上观看的视频文件格式,压缩和图像质量高,属于流媒体格式,播放器是 Media Player |
| FLV | 增长最快、最为广泛的视频传播格式,许多在线视频网站都采用此视频格式,属于流媒体格式。CPU 占用率底、视频质量良好、体积小、加载速度极快等特点 |
# 其它
对于一台计算机,一旦确定了小数点的位置就不再改变。对应的小数点在机器中是不表示出来的,而是事先约定在固定的位置。
在二进制中,每个数字称为一个比特(Bit,Binary digit 的缩写)。
常见单位:位(bit)、字节(byte/B,8bit)、KB(1024B)、M(1024KB)、GB(1024M)、T(1024GB)。
浮点数的表示中为什么要用移码表示阶码?参考信息 (opens new window)。
定点数和浮点数之间如何进行转换?
为什么 IEEE 754 标准中,阶码的偏移量是 127?参考信息 (opens new window)。
