坐标系统

OpenGL 希望在每次顶点着色器运行后，我们可见的所有顶点都为标准化设备坐标(Normalized Device Coordinate, NDC)。也就是说，每个顶点的 x，y，z 坐标都应该在-1.0 到 1.0 之间，超出这个坐标范围的顶点都将不可见。

通常我们会自己设定一个坐标的范围，之后再在顶点着色器中将这些坐标变换为标准化设备坐标。然后将这些标准化设备坐标传入光栅器，将它们变换为屏幕上的二维坐标或像素。

对我们来说比较重要的总共有 5 个不同的坐标系统：

局部空间（局部坐标）
世界空间（世界坐标）
观察空间（观察坐标）
裁剪空间（裁剪坐标）
屏幕空间（屏幕坐标）

为了将坐标从一个坐标系变换到另一个坐标系，我们需要用到几个变换矩阵，最重要的几个分别是模型、观察、投影三个矩阵。

顶点坐标起始于局部空间，在这里它称为局部坐标，它在之后会变为世界坐标，观察坐标，裁剪坐标，并最后以屏幕坐标的形式结束。下面的这张图展示了整个流程以及各个变换过程做了什么：

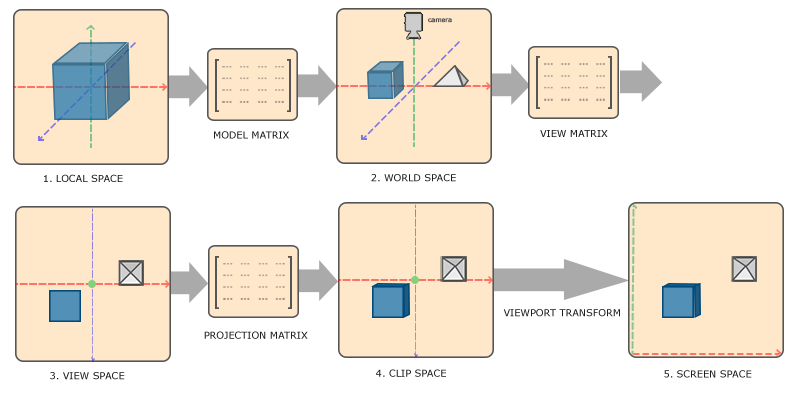
space

绘制图形

当我们想要同时绘制多个三角形时，首先我们通过指定三个顶点来分别定义一个三角形。这里其实就是在局部空间下描述了模型的形状，而每个顶点的坐标就是局部坐标。

之后，需要将我们所有的三角形导入到程序当中，它们有可能会全挤在世界的原点上（如果我们在局部空间建模时都放在原点附近的话），这并不是我们想要的结果。因此我们需要通过模型变换来让它们移动到应该所处的相对位置上，此时并来到了世界空间中。

对于摆放好的各个三角形，如果我们以不同的视角进行观察的话看到的结果也不一样，因此我们可以通过创建一个观察矩阵来模拟一个摄像机以控制观察的位置和角度，如此并来到了我们的观察空间。

在处理三维的物体时，为了将其绘制到屏幕上，我们需要先将物体投影到 2D 空间中，投影之后我们就来到了裁剪空间。具体投影的方式可以有很多种，比如透视投影、正交投影等。

投影矩阵指定了一个范围的坐标（比如在每个维度上的-1000 到 1000），接着会将在这个指定的范围内的坐标变换为标准化设备坐标的范围 (-1.0, 1.0)。所有在范围外的坐标不会被映射到在 -1.0 到 1.0 的范围之间，所以会被裁剪掉。
由投影矩阵创建的观察箱被称为平截头体（Frustum），每个出现在平截头体范围内的坐标都会最终出现在用户的屏幕上。将特定范围内的坐标转化到标准化设备坐标系的过程被称之为投影，因为使用投影矩阵能将 3D 坐标投影到很容易映射到 2D 的标准化设备坐标系中。
一旦所有顶点被变换到裁剪空间，最终的操作——透视除法将会执行，在这个过程中我们将位置向量的 x，y，z 分量分别除以向量的齐次 w 分量；透视除法是将 4D 裁剪空间坐标变换为 3D 标准化设备坐标的过程。这一步会在每一个顶点着色器运行的最后被自动执行。

在这一阶段之后，所有的顶点并都转化为了标准化设备坐标，而这些坐标将会被映射到屏幕空间中（使用 glViewport 中的设定，视口变化），最后被变换成片段。

拍照

以拍照为例，假设现在需要给一群人拍照。首先，里面每个人需要现在自己的环境里整理仪容仪表，摆出不同的造型，各自调整时所处的就是局部空间。

当每个人准备好之后，我们需要将他们先集中起来，然后调整位置和角度。集中起来的方式就是使用模型变换，而调整之后大家所在的空间就变成世界空间。

在按下快门之前，摄影师通常也会调整相机的位置和角度，以确保得到最好看的效果，整个调整过程我们可以通过观察矩阵来实现，此时我们来到了观察空间。

当按下快门之后，现实中三维的场景并成了平面照片，同时摄影机屏幕外的部分被忽略。这一投影的过程我们可以通过投影矩阵来实现，因为在相机之外的物体是不会被看到的，因此投影之后也被称作为裁剪空间。

为了将拍照的结果显示到屏幕上，我们需要将裁剪空间中的坐标（由于投影后自动执行了透视除法，所以下一步得到的将是标准化设备坐标）映射为屏幕坐标。

立方体

既然我们知道了如何将 3D 坐标变换为 2D 坐标，我们可以开始使用真正的 3D 物体了。

顶点

为了绘制一个立方体，我们一共需要 36 个顶点（6 个面 x 每个面有 2 个三角形组成 x 每个三角形有 3 个顶点）。

cpp

float vertices[] = {
    -0.5f, -0.5f, -0.5f,  0.0f, 0.0f,
    0.5f, -0.5f, -0.5f,  1.0f, 0.0f,
    0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
    0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
    -0.5f,  0.5f, -0.5f,  0.0f, 1.0f,
    -0.5f, -0.5f, -0.5f,  0.0f, 0.0f,

    -0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
    0.5f, -0.5f,  0.5f,  1.0f, 0.0f,
    0.5f,  0.5f,  0.5f,  1.0f, 1.0f,
    0.5f,  0.5f,  0.5f,  1.0f, 1.0f,
    -0.5f,  0.5f,  0.5f,  0.0f, 1.0f,
    -0.5f, -0.5f,  0.5f,  0.0f, 0.0f,

    -0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
    -0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
    -0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
    -0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
    -0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
    -0.5f,  0.5f,  0.5f,  1.0f, 0.0f,

    0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
    0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
    0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
    0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
    0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
    0.5f,  0.5f,  0.5f,  1.0f, 0.0f,

    -0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
    0.5f, -0.5f, -0.5f,  1.0f, 1.0f,
    0.5f, -0.5f,  0.5f,  1.0f, 0.0f,
    0.5f, -0.5f,  0.5f,  1.0f, 0.0f,
    -0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
    -0.5f, -0.5f, -0.5f,  0.0f, 1.0f,

    -0.5f,  0.5f, -0.5f,  0.0f, 1.0f,
    0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
    0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
    0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
    -0.5f,  0.5f,  0.5f,  0.0f, 0.0f,
    -0.5f,  0.5f, -0.5f,  0.0f, 1.0f
};

float vertices[] = {
    -0.5f, -0.5f, -0.5f,  0.0f, 0.0f,
    0.5f, -0.5f, -0.5f,  1.0f, 0.0f,
    0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
    0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
    -0.5f,  0.5f, -0.5f,  0.0f, 1.0f,
    -0.5f, -0.5f, -0.5f,  0.0f, 0.0f,

    -0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
    0.5f, -0.5f,  0.5f,  1.0f, 0.0f,
    0.5f,  0.5f,  0.5f,  1.0f, 1.0f,
    0.5f,  0.5f,  0.5f,  1.0f, 1.0f,
    -0.5f,  0.5f,  0.5f,  0.0f, 1.0f,
    -0.5f, -0.5f,  0.5f,  0.0f, 0.0f,

    -0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
    -0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
    -0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
    -0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
    -0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
    -0.5f,  0.5f,  0.5f,  1.0f, 0.0f,

    0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
    0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
    0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
    0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
    0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
    0.5f,  0.5f,  0.5f,  1.0f, 0.0f,

    -0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
    0.5f, -0.5f, -0.5f,  1.0f, 1.0f,
    0.5f, -0.5f,  0.5f,  1.0f, 0.0f,
    0.5f, -0.5f,  0.5f,  1.0f, 0.0f,
    -0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
    -0.5f, -0.5f, -0.5f,  0.0f, 1.0f,

    -0.5f,  0.5f, -0.5f,  0.0f, 1.0f,
    0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
    0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
    0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
    -0.5f,  0.5f,  0.5f,  0.0f, 0.0f,
    -0.5f,  0.5f, -0.5f,  0.0f, 1.0f
};

对应的，我们需要更新告知 OpenGL 对坐标的解析方式：

cpp

// 告诉 OpenGL 该如何解析顶点数据
glVertexAttribPointer(0 /* 指定要配置的顶点属性 */,
                        3 /* 顶点属性的大小 */,
                        GL_FLOAT /* 数据的类型 */,
                        GL_FALSE /* 是否标准化 */,
                        5 * sizeof(float) /* 步长 */,
                        (void *)0 /* 位置数据在缓冲中起始位置的偏移量 */);
// 启用顶点属性
glEnableVertexAttribArray(0);

// texture coord attribute
glVertexAttribPointer(1, 2, GL_FLOAT, GL_FALSE, 5 * sizeof(float), (void*)(3 * sizeof(float)));
glEnableVertexAttribArray(1);

// 告诉 OpenGL 该如何解析顶点数据
glVertexAttribPointer(0 /* 指定要配置的顶点属性 */,
                        3 /* 顶点属性的大小 */,
                        GL_FLOAT /* 数据的类型 */,
                        GL_FALSE /* 是否标准化 */,
                        5 * sizeof(float) /* 步长 */,
                        (void *)0 /* 位置数据在缓冲中起始位置的偏移量 */);
// 启用顶点属性
glEnableVertexAttribArray(0);

// texture coord attribute
glVertexAttribPointer(1, 2, GL_FLOAT, GL_FALSE, 5 * sizeof(float), (void*)(3 * sizeof(float)));
glEnableVertexAttribArray(1);

变换

为了让立方体看起来更真实，我们将绘制多个矩形，为此每个立方体将具有不同的模型变换矩阵：

cpp

glm::vec3 cubePositions[] = {
    glm::vec3(0.0f, 0.0f, 0.0f),
    glm::vec3(2.0f, 5.0f, -15.0f),
    glm::vec3(-1.5f, -2.2f, -2.5f),
    glm::vec3(-3.8f, -2.0f, -12.3f),
    glm::vec3(2.4f, -0.4f, -3.5f),
    glm::vec3(-1.7f, 3.0f, -7.5f),
    glm::vec3(1.3f, -2.0f, -2.5f),
    glm::vec3(1.5f, 2.0f, -2.5f),
    glm::vec3(1.5f, 0.2f, -1.5f),
    glm::vec3(-1.3f, 1.0f, -1.5f)
};

void transform(int shaderProgram, int i)
{
    // create transformations
    glm::mat4 model = glm::mat4(1.0f);
    model = glm::translate(model, cubePositions[i]);
    float angle = 20.0f * i;
    model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
    unsigned int modelLoc = glGetUniformLocation(shaderProgram, "model");
    glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));

    glm::mat4 view = glm::mat4(1.0f); // make sure to initialize matrix to identity matrix first
    view = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f));
    unsigned int viewLoc = glGetUniformLocation(shaderProgram, "view");
    glUniformMatrix4fv(viewLoc, 1, GL_FALSE, glm::value_ptr(view));

    glm::mat4 projection = glm::mat4(1.0f);
    projection = glm::perspective(glm::radians(45.0f), (float)screenWidth / (float)screenHeight, 0.1f, 100.0f);
    unsigned int projectionLoc = glGetUniformLocation(shaderProgram, "projection");
    glUniformMatrix4fv(projectionLoc, 1, GL_FALSE, glm::value_ptr(projection));
}

glm::vec3 cubePositions[] = {
    glm::vec3(0.0f, 0.0f, 0.0f),
    glm::vec3(2.0f, 5.0f, -15.0f),
    glm::vec3(-1.5f, -2.2f, -2.5f),
    glm::vec3(-3.8f, -2.0f, -12.3f),
    glm::vec3(2.4f, -0.4f, -3.5f),
    glm::vec3(-1.7f, 3.0f, -7.5f),
    glm::vec3(1.3f, -2.0f, -2.5f),
    glm::vec3(1.5f, 2.0f, -2.5f),
    glm::vec3(1.5f, 0.2f, -1.5f),
    glm::vec3(-1.3f, 1.0f, -1.5f)
};

void transform(int shaderProgram, int i)
{
    // create transformations
    glm::mat4 model = glm::mat4(1.0f);
    model = glm::translate(model, cubePositions[i]);
    float angle = 20.0f * i;
    model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
    unsigned int modelLoc = glGetUniformLocation(shaderProgram, "model");
    glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));

    glm::mat4 view = glm::mat4(1.0f); // make sure to initialize matrix to identity matrix first
    view = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f));
    unsigned int viewLoc = glGetUniformLocation(shaderProgram, "view");
    glUniformMatrix4fv(viewLoc, 1, GL_FALSE, glm::value_ptr(view));

    glm::mat4 projection = glm::mat4(1.0f);
    projection = glm::perspective(glm::radians(45.0f), (float)screenWidth / (float)screenHeight, 0.1f, 100.0f);
    unsigned int projectionLoc = glGetUniformLocation(shaderProgram, "projection");
    glUniformMatrix4fv(projectionLoc, 1, GL_FALSE, glm::value_ptr(projection));
}

着色器

为了让模型矩阵使用起来，我们需要更新着色器：

cpp

const std::string vertexString = SHADER_STRING(
    // 设定了输入变量的位置值
    layout(location = 0) in vec3 aPos;
    layout(location = 1) in vec2 aTexCoord;

    out vec2 TexCoord;

    uniform mat4 model;
    uniform mat4 view;
    uniform mat4 projection;

    void main() {
        gl_Position = projection * view * model * vec4(aPos, 1.0f);
        TexCoord = vec2(aTexCoord.x, 1.0 - aTexCoord.y);
    });

const std::string fragString = SHADER_STRING(
    // 片段着色器只需要一个输出变量，这个变量是一个 4 分量向量，它表示的是最终的输出颜色
    out vec4 FragColor;

    in vec2 TexCoord;

    uniform sampler2D ourTexture;

    void main() {
        FragColor = texture(ourTexture, TexCoord);
    });

const std::string vertexString = SHADER_STRING(
    // 设定了输入变量的位置值
    layout(location = 0) in vec3 aPos;
    layout(location = 1) in vec2 aTexCoord;

    out vec2 TexCoord;

    uniform mat4 model;
    uniform mat4 view;
    uniform mat4 projection;

    void main() {
        gl_Position = projection * view * model * vec4(aPos, 1.0f);
        TexCoord = vec2(aTexCoord.x, 1.0 - aTexCoord.y);
    });

const std::string fragString = SHADER_STRING(
    // 片段着色器只需要一个输出变量，这个变量是一个 4 分量向量，它表示的是最终的输出颜色
    out vec4 FragColor;

    in vec2 TexCoord;

    uniform sampler2D ourTexture;

    void main() {
        FragColor = texture(ourTexture, TexCoord);
    });

深度测试

OpenGL 存储它的所有深度信息于一个 Z 缓冲中，也被称为深度缓冲。GLFW 会自动为你生成这样一个缓冲。

深度值存储在每个片段里面，当片段想要输出它的颜色时，OpenGL 会将它的深度值和 z 缓冲进行比较，如果当前的片段在其它片段之后，它将会被丢弃，否则将会覆盖。这个过程称为深度测试，它是由 OpenGL 自动完成的。

cpp

glEnable(GL_DEPTH_TEST); // 开启深度测试

glEnable(GL_DEPTH_TEST); // 开启深度测试

因为我们使用了深度测试，我们也想要在每次渲染迭代之前清除深度缓冲：

cpp

glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // 清除颜色和深度缓冲

glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // 清除颜色和深度缓冲

渲染

最后，我们在循环指令中通过循环绘制多个立方体，并使用不同的模型矩阵来变换它们：

cpp

int main()
{
    // ...
    glEnable(GL_DEPTH_TEST);

    // 渲染循环
    while (!glfwWindowShouldClose(window)) // 检查一次 GLFW 是否被要求退出
    {
        // ...
        // 渲染指令
        glClearColor(0.2f, 0.3f, 0.3f, 1.0f);
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // 清除颜色和深度缓冲
        glBindTexture(GL_TEXTURE_2D, texture);
        CHECK_GL(glUseProgram(shaderProgram));
        glBindVertexArray(VAO);
        for (unsigned int i = 0; i < 10; i++) // 绘制多个立方体
        {
            transform(shaderProgram, i);
            glDrawArrays(GL_TRIANGLES, 0, 36);
        }
        // ...
    }
    // ...
}

int main()
{
    // ...
    glEnable(GL_DEPTH_TEST);

    // 渲染循环
    while (!glfwWindowShouldClose(window)) // 检查一次 GLFW 是否被要求退出
    {
        // ...
        // 渲染指令
        glClearColor(0.2f, 0.3f, 0.3f, 1.0f);
        glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // 清除颜色和深度缓冲
        glBindTexture(GL_TEXTURE_2D, texture);
        CHECK_GL(glUseProgram(shaderProgram));
        glBindVertexArray(VAO);
        for (unsigned int i = 0; i < 10; i++) // 绘制多个立方体
        {
            transform(shaderProgram, i);
            glDrawArrays(GL_TRIANGLES, 0, 36);
        }
        // ...
    }
    // ...
}

现在，你应该会看到多个立方体了。

坐标系统 ​

绘制图形 ​

拍照 ​

立方体 ​

顶点 ​

变换 ​

着色器 ​

深度测试 ​

渲染 ​

坐标系统

绘制图形

拍照

立方体

顶点

变换

着色器

深度测试

渲染